Deep dive into bits, bytes, shorts, ints, longs, signed, and unsigned with Java
On the Pi4J discussion list, someone recently asked what the best and easiest way is in Java to convert a byte value. In Java, there is no distinction between signed and unsigned bytes, which can be confusing. My book “Getting Started with Java on the Raspberry Pi” contains an explanation about this, and I am happy to share it in this post with some more info and code examples…
You can find all the code of this post on GitHub.
The Basics: Bits
Let’s start with the basics: bits, 0 or 1.
A bit (binary digit) is the smallest unit of data in a computer, and has two possible values: 0 or 1. Bits are the foundation of everything that happens in a computer. All instructions or data stored in memory are represented as combinations of bits. Bits are mostly grouped together into larger units such as bytes or words, so they can represent numbers, characters, or control signals, depending on the context in which they are used.
In everyday life, we are used to decimal values where we group everything by 10, 20, 30,… In programming, hexadecimal (or hex) values are often used, which group numbers by sixteen. Hexadecimal values range from 0 to 15, which matches perfectly with the maximum value of four bits (1111 in binary). Each hex digit can represent a value from 0 to F, where F is 15 in decimal. A hex value is typically written as 0x0 to 0xF to distinguish it from decimal notation.
Each binary digit (bit) represents a power of 2, starting from the rightmost bit (which is 2^0) and moving left. The value of the binary number is the sum of the powers of 2 where there is a bit 1.
The following table shows all possible combinations of 4 bits ranging from “0000” to “1111”.
| Bits | 2^3 | 2^2 | 2^1 | 2^0 | + | Number | HEX |
|---|---|---|---|---|---|---|---|
| 8 | 4 | 2 | 1 | ||||
| 0000 | 0 | 0 | 0 | 0 | 0+0+0+0 | 0 | 0x0 |
| 0001 | 0 | 0 | 0 | 1 | 0+0+0+1 | 1 | 0x1 |
| 0010 | 0 | 0 | 1 | 0 | 0+0+2+0 | 2 | 0x2 |
| 0011 | 0 | 0 | 1 | 1 | 0+0+2+1 | 3 | 0x3 |
| 0100 | 0 | 1 | 0 | 0 | 0+4+0+0 | 4 | 0x4 |
| 0101 | 0 | 1 | 0 | 1 | 0+4+0+1 | 5 | 0x5 |
| 0110 | 0 | 1 | 1 | 0 | 0+4+2+0 | 6 | 0x6 |
| 0111 | 0 | 1 | 1 | 1 | 0+4+2+1 | 7 | 0x7 |
| 1000 | 1 | 0 | 0 | 0 | 8+0+0+0 | 8 | 0x8 |
| 1001 | 1 | 0 | 0 | 1 | 8+0+0+1 | 9 | 0x9 |
| 1010 | 1 | 0 | 1 | 0 | 8+0+2+0 | 10 | 0xA |
| 1011 | 1 | 0 | 1 | 1 | 8+0+2+1 | 11 | 0xB |
| 1100 | 1 | 1 | 0 | 0 | 8+4+0+0 | 12 | 0xC |
| 1101 | 1 | 1 | 0 | 1 | 8+4+0+1 | 13 | 0xD |
| 1110 | 1 | 1 | 1 | 0 | 8+4+2+0 | 14 | 0xE |
| 1111 | 1 | 1 | 1 | 1 | 8+4+2+1 | 15 | 0xF |
This video by Mathmo14159 very nicely illustrates how this works.
And we can achieve the same result with the following Java code:
System.out.println("Value\tBits\tHex");
for (int i = 0; i <= 15; i++) {
System.out.println(i
+ "\t" + String.format("%4s", Integer.toBinaryString(i)).replace(' ', '0')
+ "\t0x" + Integer.toHexString(i).toUpperCase());
}
// Output
Value Bits Hex
0 0000 0x0
1 0001 0x1
2 0010 0x2
3 0011 0x3
4 0100 0x4
5 0101 0x5
6 0110 0x6
7 0111 0x7
8 1000 0x8
9 1001 0x9
10 1010 0xA
11 1011 0xB
12 1100 0xC
13 1101 0xD
14 1110 0xE
15 1111 0xF
Bits to Byte
A byte consists of 8 bits and has the range of 0x00 (= 0) to 0xFF (= 255).
So we need to extend the table above to have 8 bits. Let’s take a few examples:
| Bits | 2^7 | 2^6 | 2^5 | 2^4 | 2^3 | 2^2 | 2^1 | 2^0 | + | Total | HEX |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||||
| 00000001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | x01 |
| 00000010 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 2 | x02 |
| 00000011 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2+1 | 3 | x03 |
| 00000100 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 4 | 4 | x04 |
| 00001111 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 8+4+2+1 | 15 | x0F |
| 00011111 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 16+…+1 | 31 | x1F |
| 00100000 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 32 | 32 | x20 |
| 11111111 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 128+…+1 | 255 | xFF |
Again, outputting the same with Java code:
System.out.println("Value\tBits\tHex");
for (int i = 0; i <= 255; i++) {
System.out.println(i
+ "\t" + String.format("%8s", Integer.toBinaryString(i)).replace(' ', '0')
+ "\t0x" + Integer.toHexString(i).toUpperCase());
}
// Output
Value Bits Hex
0 00000000 0x0
1 00000001 0x1
2 00000010 0x2
3 00000011 0x3
...
15 00001111 0xF
16 00010000 0x10
17 00010001 0x11
...
253 11111101 0xFD
254 11111110 0xFE
255 11111111 0xFF
Value Ranges in Java
A bit doesn’t really exist as a data type in Java. However, the closest match is a boolean type, which can represent two states: true (equivalent to 1) and false (equivalent to 0). To store numeric whole values (without decimals), Java provides different primitive types, each with its own range and characteristics.
Difference between Byte, Short, Integer and Long
All these are numeric objects and each uses a fixed number of bytes in memory:
| Type | N° of bits | N° of bytes | Minimum | Maximum |
|---|---|---|---|---|
| byte | 8 | 1 | 0x00 | 0xFF |
| short | 16 | 2 | 0x0000 | 0xFFFF |
| int | 32 | 4 | 0x00000000 | 0xFFFFFFFF |
| long | 64 | 8 | 0x0000000000000000 | 0xFFFFFFFFFFFFFFFF |
Minimum and maximum values in Java
Let’s go back to Java and check how values are represented with the following code:
System.out.println("Byte");
System.out.println(" Min: " + Byte.MIN_VALUE);
System.out.println(" Max: " + Byte.MAX_VALUE);
System.out.println("Short");
System.out.println(" Min: " + Short.MIN_VALUE);
System.out.println(" Max: " + Short.MAX_VALUE);
System.out.println("Integer");
System.out.println(" Min: " + Integer.MIN_VALUE);
System.out.println(" Max: " + Integer.MAX_VALUE);
System.out.println("Long");
System.out.println(" Min: " + Long.MIN_VALUE);
System.out.println(" Max: " + Long.MAX_VALUE);
As a result, we get these values:
Byte
Min: -128
Max: 127
Short
Min: -32768
Max: 32767
Integer
Min: -2147483648
Max: 2147483647
Long
Min: -9223372036854775808
Max: 9223372036854775807
Hmm, this is unexpected! Does a byte have the range of -128 to 127, instead of 0 to 255?! That’s why we need to understand the difference between signed and unsigned values.
Signed versus Unsigned
- Signed Byte: The most significant bit (MSB = the most left one) is used as the sign bit, indicating whether the value is positive or negative. This results in a range for a byte of -128 to 127.
- Unsigned Byte: All bits are used for the value, without a sign bit. This results in a range for a byte of 0 to 255.
Java does not have a native unsigned byte type, but you can achieve unsigned behavior by treating a byte as an int or using bitwise operations.
When you calculate the byte value to a signed number value, the major bit (the most left one) is handled as an indicator for a negative number (1) or a positive number (0). Let’s try a few examples:
System.out.println("Bits to byte");
System.out.println("Byte value 00000001: " + ((byte) Integer.parseInt("00000001", 2)));
System.out.println("Byte value 00001111: " + ((byte) Integer.parseInt("00001111", 2)));
System.out.println("Byte value 01111111: " + ((byte) Integer.parseInt("01111111", 2)));
System.out.println("Byte value 10000000: " + ((byte) Integer.parseInt("10000000", 2)));
System.out.println("Byte value 10000001: " + ((byte) Integer.parseInt("10000001", 2)));
System.out.println("Byte value 10001111: " + ((byte) Integer.parseInt("10001111", 2)));
// Output
Bits to byte
Byte value 00000001: 1
Byte value 00001111: 15
Byte value 01111111: 127
Byte value 10000000: -128
Byte value 10000001: -127
Byte value 10001111: -113
Using Masks
A mask is a value used in bitwise operations to extract or manipulate specific bits of another value. By applying a mask in the format byte & 0xFF, we can convert a byte value to it’s unsigned integer value. By applying the mask 0xFF, which has only 8 bits, you effectively keep only the lower 8 bits of the byte value when it’s converted to an integer.
As you can see from the following code example, applying a mask converts a byte to an integer, and shows the unsigned value for 10001111.
System.out.println("Byte to Integer with mask");
var b = (byte) Integer.parseInt("10001111", 2);
System.out.println("Byte value: " + b);
var bWithMask = b & 0xff;
System.out.println("Byte value with mask: " + bWithMask);
System.out.println("Object Type: " + printObjectType(bWithMask));
// Helper method to show the type of object
private static String printObjectType(Object obj) {
if (obj != null) {
return obj.getClass().getName();
} else {
return "NULL";
}
}
// Output
Byte value: -113
Byte value with mask: 143
Object Type: java.lang.Integer
Using Helper Methods
Applying a mask is a short piece of code and you can easily add it to your code to convert a signed byte to its unsigned integer equivalent. However, there are also built-in helper methods available in Java that return the same result but are more readable. This is important for code reviews or when you or someone else need to mainten or extend the code: Byte.toUnsignedInt(b) and Byte.toUnsignedLong(b).
System.out.println("Byte to Integer with toUnsignedInt");
var unsignedInt = Byte.toUnsignedInt(b);
System.out.println("Byte to unsigned integer: " + unsignedInt);
System.out.println("Object Type: " + printObjectType(unsignedInt));
// In case you need it as a Long...
System.out.println("Byte to Long with toUnsignedLong");
var unsignedLong = Byte.toUnsignedLong(b);
System.out.println("Byte to unsigned long: " + unsignedLong);
System.out.println("Object Type: " + printObjectType(unsignedLong));
// Output
Byte to Integer with toUnsignedInt
Byte to unsigned integer: 143
Object Type: java.lang.Integer
Byte to Long with toUnsignedLong
Byte to unsigned long: 143
Object Type: java.lang.Long
Same Approach for Short
A short in Java uses 16 bits (or 2 bytes) and can be handled similarly when converting from its binary representation. A short is also a signed data type, with a range of -32,768 to 32,767.
System.out.println("Example with short");
short s1 = (short) Integer.parseInt("1000000000000000", 2);
System.out.println("Short value 1000000000000000: " + s1);
System.out.println("Short value 1000000000000000 with mask: " + (s1 & 0xFFFF));
System.out.println("Using Short.toUnsignedLong: " + Short.toUnsignedInt(s1));
short s2 = (short) Integer.parseInt("1111111111111111", 2);
System.out.println("Short value 1111111111111111: " + s2);
System.out.println("Short value 1111111111111111 to unsigned: " + Short.toUnsignedInt(s2));
// Output
Example with short
Short value 1000000000000000: -32768
Short value 1000000000000000 with mask: 32768
Using Short.toUnsignedLong: 32768
Short value 1111111111111111: -1
Short value 1111111111111111 to unsigned: 65535
Example use of Bits
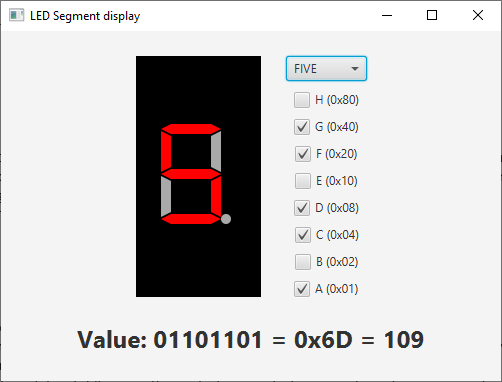
A nice example of the use of bits and bytes, is included in my book. A LED number display is a typical component used in a lot of experiments with electronics and is also used in e.g. alarm clocks. Such a display has 7 segments to for the number, and one for the dot. So a total of 8 true/false values to define what must be displayed. This makes it the perfect example of how 8 booleans can be combined into one byte.
In 2019, I even published a JavaFX library with a component to visualize such a display, as you can read here: “LED number display JavaFX library published on Maven”.
Conclusion
Understanding how to work with bits, bytes and shorts in Java is essential for effective programming, especially when dealing with low-level data manipulation for electronic components, such as with Raspberry Pi and Pi4J projects. The way Java handles signed data types can sometimes be confusing, but by using masks and/or the helper methods like Byte.toUnsignedInt() and Short.toUnsignedInt(), you can efficiently convert these values.
Remark
This is a returning question, so also this blog post is not completely new ;-) A shorter version was published on October 25, 2019. I created this new post to provide deeper explanation, a video, and more Java code examples.